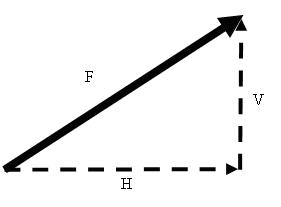
Remember that if you have a force that goes at an angle, you can take components in the horizontal and vertical directions.
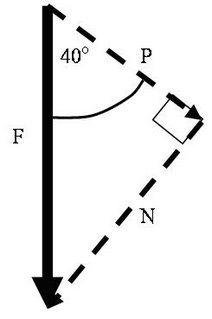The problem comes when the actual force is either vertical or horizontal in the first place. You might think that there is no point in taking components.However, what if the driving force is the gravitational pull, or weight, and we want the object to move at 40 degrees to the vertical instead of straight down? The answer is that we can come up with components in these directions as long as they make a right angled triangle.
Which brings us to the example below. The ball moves in the direction dictated by the direction of the curve but the only force on it is weight pulling vertically downwards:
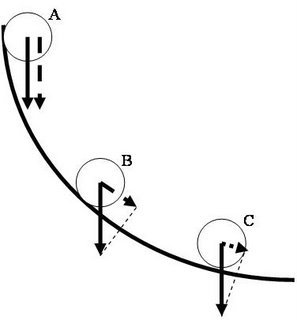
The driving force becomes the component pointing in the direction of the gradient. We do components at A, B and C using the method outlined above.
Notice that in order to keep a right angled triangle, the size of the component becomes progressively smaller. Hence the acceleration decreases in magnitude (size).
In other words, the ball continues to speed up but not by as much each time. It will reach constant speed when the slope becomes horizontal because gravity will no longer be able to make it accelerate.
