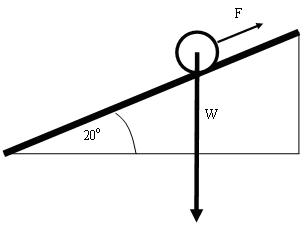
This is a picture of a ball going up a slope at a constant speed.If it going at constant speed, then
driving force = counter force
Driving force is F, because it is pointing in the direction of motion, by Newton's Second Law which says "Rate of change of momentum is proortional to the resultant force and that change in momentum is in the direction of the resultant force".
However, although gravity is making it harder for the ball to go up the slope, the weight W is NOT the counter force because it is not in line with the motion.
We need to take components of W:
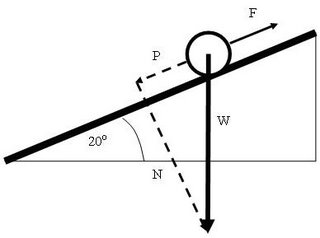Notice that this has been done using the method set out in my previous post.Just in case you were wondering, P stands for parallel to the slope and N stands for normal to the slope.
Lastly we need to look in detail at the components:
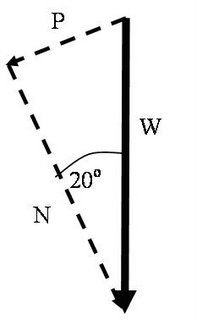
Notice that the bottom angle is the same as the angle for the slope.
By Pythagoras,
P = W sin20
P is the counter force because it is in exactly the opposite direction to the motion (and thus the change in momentum)
Finally, since
Driving force = counter force
F = P
F = W sin20
An example of this type of question might say:
"An object of mass 50 kg travels up a slope of angle 20 degrees at a constant speed of 5 m/s. What is the power output needed to maintain the motion?"
You will of course remember that power output P = Fv. It's on the data sheet.
Hence we already know v, we have to find F
F = W sin 20 but weight W = mg = 50 x 9.81 = 490.5 Newtons
F = 490.5 x sin20 = 167.8 Newtons
Hence power output = Fv = 167.8 Newtons x 5 m/s = 839 Watts to 3 sig fig
One final point: If you have had to put your calculator into RADIANS for maths, make sure you put it back into DEGREES.
