Applying Newton's Laws to terminal velocity

Think about the freee fall parachutist example:

At first, the only force acting on her is her weight. She has no air resistance at first because her initial speed is zero.

Hence she has a resultant force downwards. Newton's Second Law states that rate of change of momentum is proportional to reultant force, so she accelerates.

As her velocity increases in magnitude, her weight remains constant but her air resistance increases. This means that her resultant force is still downwards but decreases in size. She still accelerates, but she does not gain as much speed each time.

Eventually, the air resistance is the same size as the weight. Resultant force is zero. Newton's First law says that objects continue with uniform motion (straight line, constant speed to you) unless an external resultant force acts. No resultant force thus means constant speed.

When she opens her parachute, her weight remains the same but the air resistance increases greatly. This gives her a resultant force upwards. The second part of Newton's Second Law states that the change in momentum takes place in the direction of the resultant force. If you have momentum downwards but the change is upwards, you must slow down.

As she slows down, her air resistance decreases, but her weight stays the same. Hence her resultant force upwards decreases. She continues to slow down but not by as much each time.

Eventually, she has slowed so much that the size of the air resistance is the same as her weight. Once again she goes at constant speed by Newton's First Law. However, this time it is a smaller terminal velocity so she does not get hurt when she hits the ground.

More about the ball on the curve

In the ball on the curve problem, you were asked to calculate the speed of the ball when it reached the bottom of the curve, given the vertical height of the curved section:

The temptation would be to use suvat by saying that the acceleration was 9.81m/s2 and that the distance s was given by h.

This would be the wrong thing to do because 9.81 is only the acceleration at A.

At B, it is the dotted component that points in the direction of motion that causes the acceleration. This is smaller than the weight, so the acceleration has reduced.

And at the end, when the ball is moving horizontally, it no longer accelerates at all.

So to solve the problem, we use an energy argument:

Say that gravitational potential energy at the top = kinetic energy at the bottom

assuming that no energy has been wasted by a transformation into thermal energy by friction.

Thus





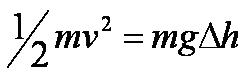
And

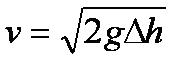
Falling from the Eiffel Tower

When you are at the top of the Eiffel Tower you have gravitational potential energy.





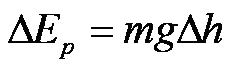
As you fall, your gravitational potential is transformed into kinetic energy.






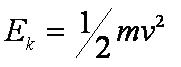
Now assuming that there is no air resistance to transform any of the kinetic energy into thermal (heat) energy due to friction, your gravitational potential energy at the top will be equal to your kinetic energy at the bottom. This is because all of the energy will have been transferred.

You would get this equation:





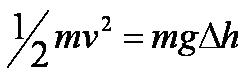
But now we can cancel the mass:






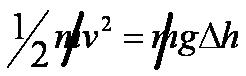
Finally we can rearrange what is left to get an equation for the velocity v when you hit the ground:


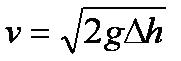
Notice that v does not depend on the mass of the object, because that cancelled out. Hence all objects will hit the ground at the same speed if there is no air resistance.

Constant speed up a slope

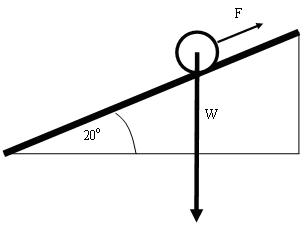This is a picture of a ball going up a slope at a constant speed.

If it going at constant speed, then

driving force = counter force

Driving force is F, because it is pointing in the direction of motion, by Newton's Second Law which says "Rate of change of momentum is proortional to the resultant force and that change in momentum is in the direction of the resultant force".

However, although gravity is making it harder for the ball to go up the slope, the weight W is NOT the counter force because it is not in line with the motion.

We need to take components of W:

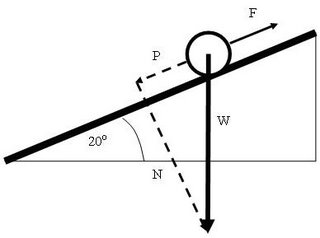Notice that this has been done using the method set out in my previous post.

Just in case you were wondering, P stands for parallel to the slope and N stands for normal to the slope.








Lastly we need to look in detail at the components:



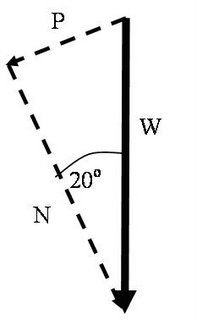
Notice that the bottom angle is the same as the angle for the slope.

By Pythagoras,

P = W sin20




P is the counter force because it is in exactly the opposite direction to the motion (and thus the change in momentum)







Finally, since

Driving force = counter force

F = P

F = W sin20


An example of this type of question might say:
"An object of mass 50 kg travels up a slope of angle 20 degrees at a constant speed of 5 m/s. What is the power output needed to maintain the motion?"

You will of course remember that power output P = Fv. It's on the data sheet.

Hence we already know v, we have to find F

F = W sin 20 but weight W = mg = 50 x 9.81 = 490.5 Newtons

F = 490.5 x sin20 = 167.8 Newtons

Hence power output = Fv = 167.8 Newtons x 5 m/s = 839 Watts to 3 sig fig

One final point: If you have had to put your calculator into RADIANS for maths, make sure you put it back into DEGREES.

past papers

This should be a working link to the past papers section of the AQA website. We are physics syllabus A and we are studying module 2 at the moment:

http://www.aqa.org.uk/qual/gceasa/phya_assess.html

Ball on a curved surface

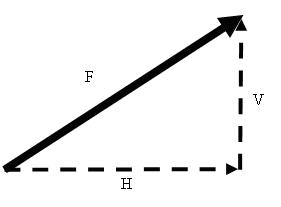
Remember that if you have a force that goes at an angle, you can take components in the horizontal and vertical directions.









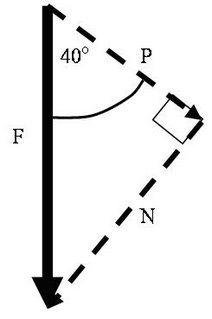The problem comes when the actual force is either vertical or horizontal in the first place. You might think that there is no point in taking components.

However, what if the driving force is the gravitational pull, or weight, and we want the object to move at 40 degrees to the vertical instead of straight down? The answer is that we can come up with components in these directions as long as they make a right angled triangle.










Which brings us to the example below. The ball moves in the direction dictated by the direction of the curve but the only force on it is weight pulling vertically downwards:


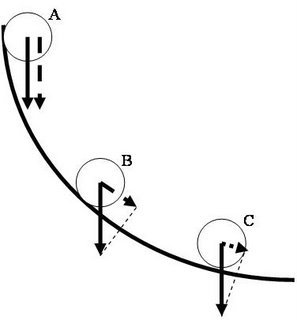
The driving force becomes the component pointing in the direction of the gradient. We do components at A, B and C using the method outlined above.

Notice that in order to keep a right angled triangle, the size of the component becomes progressively smaller. Hence the acceleration decreases in magnitude (size).

In other words, the ball continues to speed up but not by as much each time. It will reach constant speed when the slope becomes horizontal because gravity will no longer be able to make it accelerate.

Applying Newton's Laws

Remember the very pedantic approach to why a door opens when you kick it.

Your foot hits the door.

The door exerts a force on foot to stop it.

Hence the foot experiences a change in momentum in accodance with Newton's Second Law: The resultant force is proportional to the rate of change of momentum.

However, Newton's Third Law states that: If object A exerts a force on object B, then object B exerts an equal force of the same type on object A in the opposite direction.

Hence there is a reaction force from the foot on the door.

It is this reaction force that then causes a change in momentum forwards on the door to open it, in accordance with Newton's Second Law.

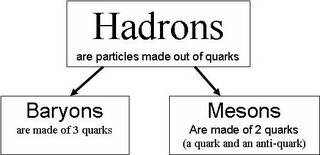
Matter that is made out of quarks

Exam questions will basically deal with up, down and strange quarks.

Remember that in any interaction, the baryon number on the left must be same as the baryon number on the right. Strangeness does not have to be conserved.

Four fundamental forces

All forces in physics can be reduced to these four:

In line with quantum theory, which says that everything has to come in lumps, the forces work by the exchange of particles (lumps).

The particles are called gauge bosons and they are called virtual particles because they only exist as messengers between two particles carrying the force. They can never exist on their own because they would be meaningless.

To imagine repulsion caused by exchanging particles, think of two skaters approaching each other on ice.

· A throws a heavy ball to B.
· Conservation of momentum means that A is pushed away from B.
· B catches the ball from A.
· Conservation of momentum means that B is pushed away from A.

Feynman diagrams

This is for people who are re-sitting module 1.

Remember that a Feynman diagram shows the way that particles interact:




This example shows two protons repelling each other. Remember that a photon of an electromagnetic wave is the particle that carries the force for electromagnetic forces.








We start to read this example in the bottom left hand corner. A single neutro appears. Then something happens that produces a proton and two other particles. The neutron must have decayed.

The other two particles are created from a W-. This is the particle responsible for the weak nuclear force.

This example is called beta decay, because the electron produced is ejected from the nucleus.



This is another version of the same beta decay. This time it shows the quarks that make up the neutron at the start. It allows us to see that beta decay causes one of the quarks to change flavour.

The Pressure Law

This is for the case when you have

• Fixed mass of gas
  Constant Volume

When we did the experiment in class, this is what we got:

We extended the line backwards to the point at which there was zero pressure. If the pressure is zero then the molecules are no longer moving and are thus unable to crash into the walls of the container. Each molecule has zero kinetic energy. Using the rule:

Average kinetic energy of one molecule = 3/2 kT

Zero kinetic energy will mean zero temperature. So we call this point (-273oC) ABSOLUTE ZERO.

Finally we can re-plot the graph with a temperature scale in Kelvin starting from Absolute Zero.

Now we have a proportional pattern and we can conclude that:

• Pressure is proportional to absolute temperature
• Double the Kelvin temperature, double the pressure
• p/T = a constant
• p1/T1 = p2/T2

Charles' Law

This is for the case when you have

• Fixed mass of gas
• Constant pressure

When we did the experiment in class, this is what we got:

The above graph looks strange because we could only do a range of temperatures from ice to steam.

Next we extended the line backwards until we had zero volume. You can't have less than zero volume so it must have the lowest possible temperature, ABSOLUTE ZERO.

Finally, we have the case where a new temperature scale is invented starting at ABSOLUTE ZERO. This graph passes through the origin (because we moved the origin!) so we get a proportional pattern

It means

• Volume is proportional to absolute (Kelvin) temperature
• Double the Kelvin temperature, double the volume
• V/T = a constant
• V1/T1 = V2/T2

It is explained by saying that molecules are moving faster at a higher temperature so they spread further apart.

Be prepared to draw extra lines on the graph through absolute zero for

• Higher constant pressure
• Lower constant pressure

Boyle's Law

Remember that for an ideal gas there are 4 large scale measurable properties:

• Total mass of the gas
• Pressure of the gas
• Temperature of the gas
• Volume of the gas

Boyle's Law is the rule for a fixed mass of gas at constant temperature.

Here is the graph to show how volume varies with pressure:

It's not rocket science. High pressure means that you are squeezing the the gas so the volume must go down.

The mathematical pattern is:

• Volume is inversely proportional to pressure
• pV = a constant
• p1V1 = p2V2
• Double the pressure, halve the volume

You need to know how to draw further curves on the graph

• Above the existing curve for higher temperature - the particles will be moving faster pushing outwards into a bigger volume and causing more pressure
• Below the existing curve for lower temperature

Electric power question

The question that you were set was about a hairdryer with two heating wire coils in parallel. The first part about calculating the length of the wire went well. It was 3 metres. You then calculated the power of R1 which was 300 Watts (to 1 sig fig)

In the second part, it said that wire 2 was then connected in parallel and there was 3 x the power used.

This is the easy way to solve it.

Three times the power means a combined output of 900 Watts. But R1 is already giving out 300 Watts so R2 must give out 600 Watts.

R2 on its own has twice the power of R1, but the supply voltage is the same.

P=IV

So twice the power means twice the current.

If twice as much current is getting through, then wire 2 must have half the resistance.

Half the resistance means half the length.

Wire 2 is 1.5 metres.

Specific heat capacity

Specific heat capacity is the amount of energy needed to make the temperature of 1 kg of water go up by 1 Kelvin.

Note that the size of 1 Kelvin is actually the same as 1 Celsius. Temperature changes are the same whether they are measured in Celsius or kelvin.

So in specific heat capacity questions you don't need to change the temperatures into Kelvin.

The formula is on the data sheet.

They will either give you the specific heat capacity in the question or give you enough data to calculate it.

Past papers

You can get copies of past papers and mark schemes from the AQA website. We are studying Physics Syllabus A.

http://www.aqa.org.uk/qual/gceasa/phyA_assess.html

If you want to see the syllabus, you can click on "Specifications" at the top of the page. The 2007 syllabus is available as an Adobe file. You were given a hard copy of the syllabus, but it may be that your filing is terrible.

You want the bits called Subject Content
AS Module 2
AS Module 3

(and AS module 1 if you are re-sitting the January exam)

The syllabus is a useful list of things you need to revise.

Resultant force

When they use the words "resultant force" in an exam question, they want you to talk about the balance between the driving force and the counter force on an object. They then want you to link it with the equation for Newton's Second Law:

Resultant force = mass x acceleration

F = ma

A favourite example is an object falling through air.

• At first, the only force is gravity(weight) downwards. It is not yet going fast enough for there to be air resistance. Gravity is the winner and hence the resultant force is downwards. There is a resultant force so the object accelerates, going faster.
• A faster object has more air resistance.
• The weight of the object does not change. So the force downwards stays the same whilst the the counter force upwards keeps increasing.
• The resultant force gets smaller and smaller. The objects keeps accelerating but the speed goes up by less and less each time.
• Eventually air resistance upwards = weight downwards.
• There is ZERO resultant force.
• There is NO acceleration.
• The object stays at the same speed, TERMINAL VELOCITY.